Causality02-Assumptions¶
本页统计信息
-
本页约 1953 个字, 预计阅读时间 7 分钟。
-
本页总阅读量次
1. Ignorability and Exchangeability¶
上一节中我们提到了,不能简单地认为\(\mathbb{E}[Y_i(1)]-\mathbb{E}[Y_i(0)]=\mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0]\)来计算ATE,那么我们是不是可以做出一些假设,使这个等式成立呢? 答案是有的,这就是潜在结果框架中的一个很重要的假设,叫做可忽略性(Ignorability),也叫做可交换性(Exchangeability),这个假设可以形式化地表示为:
这个假设就像是在医学实验中忽略了人们最终是如何选择他们所选择的治疗方法的,而只是假设他们是被随机分配的治疗方法。用概率图来解释的话,就如下图所示:
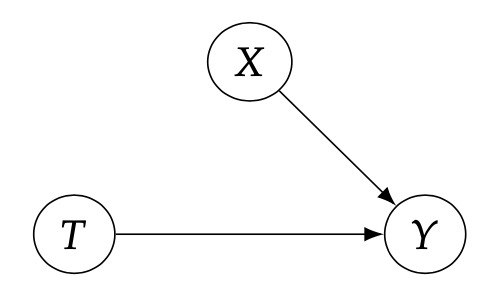
可以理解为这一假设取消了混淆变量对治疗方案T的选取的影响,将医学实验变成了纯随机的选择,有了这样的假设之后,\(\mathbb{E}[Y_i(1)]-\mathbb{E}[Y_i(0)]=\mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0]\)就成立了。 这一假设的另一个视角是可交换性。可交换性意味着治疗组是可交换的,即如果它们被交换,新的治疗组将观察到与旧的治疗组相同的结果,而新的对照组与旧的对照组也可以观察到相同的结局,这其实也在说明,treatment的选择和其他因素无关,是完全随机进行的。这个视角实际上可以理解为这样两个等式:
从这里我们可以进一步推出\(\mathbb{E}[Y(1)|T=t]=\mathbb{E}[Y(1)]\)和\(\mathbb{E}[Y(0)|T=t]=\mathbb{E}[Y(0)]\),这意味着我们可以用已经观察到的数据分布\(P(X,T,Y)\)来计算T对Y的因果效应。 虽然可忽略性假设对我们很重要,也在很大程度上可以简化因果效应的计算,但是在绝大多数时候,这个假设实际上是不成立的,现实世界中待研究的问题往往会有一些混淆因素在里面,他们对结果的影响很多时候是不能忽略的,因此,我们需要一些更弱的假设,才能避免建模的失真。
2. Conditional Exchangeability and Unconfoundedness¶
根据上文所述,我们在现实世界中很难找到完全满足Ignorability假设的场景,我们不能期望每个unit对应的混淆变量X对T和Y的影响都相同(因为是随机试验),但是在给定了X的情况下,我们可以假设治疗方案T和结果Y之间是互相独立的,这就是条件可交换性(Conditional Exchangeability),它可以用下面的公式来表示:
这个想法是,尽管治疗和潜在结果可能是无条件相关的(由于混杂),但在给定X的情况下,它们是不相关的。换句话说,我们如果控制了X保持一定,那么不同的对照组之间就是可以比较的,这个过程可以用下面这张图来解释:
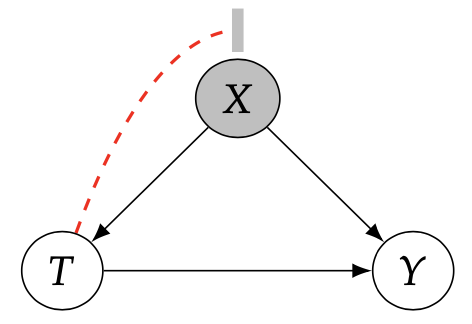
相比于原本的因果图(X对T和Y都有影响),我们进行了一种操作(书上称为do操作),这样一来,我们在给定X的情况下,T和Y的非因果关系就被blocked了,因此T和Y就不再存在非因果的关联,这样一来,在给定X的情况下,T对Y的因果效应就可以做如下计算:
对全体数据上T对Y的因果效应来说,我们可以进一步推导出:
只需要对所有可能的X求对应的条件因果效应的期望就可以了。条件可交换性是因果推断中非常重要的一个假设,这个假设也被叫做unconfoundedness假设,因为我们在计算因果效应的过程中解除了混淆变量的影响。看起来,条件可交换性比可交换性更贴合实际一点,但是也不是很多。因为我们可能有一些未观测到的混淆变量,他们不是X的一部分,而当我们考虑给定X的时候,这些未被观测到的混淆变量实际上就被忽略了,这是我们在观察数据中必须始终注意的问题。直观地说,我们能做的最好的事情是观察并尽可能多地将协变量拟合到X里面,以试图保证unconfoundedness假设的假设是成立的。
3 Positivity/Overlap and Extrapolation¶
Positivity(正值假设)是潜在结果框架中另一个重要的假设,它的含义是数据中的所有拥有不同的混淆变量X的分组,他们获得不同的treatment的结果是一定的。这个假设用公式可以表示为:
为什么这个假设这么重要呢?我们可以通过一个简单的推导来说明。首先,我们已经有了这样一个结果:
这是条件可交换性假设下因果效应的计算公式,我们根据条件概率的基本性质对其进行展开,可以得到上面的表达式又等价于:
再根据贝叶斯定理,我们可以得到:
这样一来,原本的推导结果就可以转化成:
这样一来,我们发现,\(P(T=t\mid X=x)\)出现在分母中,如果对于某些x,这个条件概率等于0的话,因果效应实际上就无法计算了,所以潜在结果框架中做出了这样的假设,就是对于所有可能的混淆量x,它对应受到的不同类型treatment的概率都必须大于0 以上是从数学的角度作出的分析,其实我们直观上也可以分析出为什么必须要有这个假设,还是以医学试验为例,如果我们对某些特定条件的受试者(比如60岁以上)都采取A方案治疗而不使用B方案,那么对于这些受试者来说,我们是无法估计不同的治疗方案的因果效应的,因为B方案的治疗在试验中根本没有出现,我们要保证每种治疗方案都被用在各种各样的病人群体上,才能准确评估这些治疗方案对全体病人的因果效应(的期望)。
Positivity假设也被叫做overlap,这个叫法其实也可以很直观地来理解,就是我们希望试验组的混淆量X的分布和对照组的相同,即\(P(X|T=1)=P(X|T=0)\)
引入更多的混淆(协变量X)更容易导致Unconfoundedness假设不成立,同时也更容易导致Positivity的假设不成立,当我们增加协变量的维度时,我们使协变量的任何水平x的子组变小。随着每个子组的变小,整个子组都得到某个治疗方案的机会越来越大,这就会导致Positivity不成立。
4. No interference, Consistency, and SUTVA¶
其实我们在介绍上面两种假设的时候,已经使用了一些基本的共通的假设,这一节主要就是详细介绍这几个假设。
4.1 No Interference¶
无干扰假设(No Interference)这个假设的是说,不同的unit之间进行的treatment互相不影响,也就是我们对不同受试者采取的治疗方案不会影响到其他受试者的实验结果。这个假设可以形式化地表述为:
4.2 Consistency¶
一致性假设(Consistency)说的是treatment T和潜在结果Y是对应的,也就是说,给定\(T=t\),那么潜在结果Y应该是\(Y(t)\),也就是说:
4.3 SUTVA¶
stable unit-treatment value assumption(SUTVA)假设在一些书上也会出现说,实际上它就是无干扰假设和一致性假设的组合。
4.4 总结¶
综上所述,在潜在结果框架中,我们一共有这样四个基本的假设: - Unconfoundedness - Positivity - No interference - Consistency 在真实的因果效应计算中,我们需要学习一个估计器(estimator)将数据集映射成对应的估计量,在机器学习中,这个估计器往往是一个模型,用来计算\(P(Y|T,X)\),这就是model-assisted estimator,面对一个真实的数据集,我们可以用下面的方法来估计ATE:
我们要做的就是使用机器学习模型来预测\(\mathbb{E}\left[Y \mid T=t, X=x_i\right]\),很显然,机器学习模型是可以做到的。